Differenza tra direttamente proporzionale e inversamente proporzionale

La proporzionalità diretta è una relazione tra due grandezze che assumono valori il cui rapporto è costante. In simboli diciamo che y è direttamente proporzionale a x se y/x=c o in modo equivalente se y=cx, con c come costante.

La proporzionalità inversa è una relazione in cui due grandezze assumono valori il cui prodotto è costante. In simboli, diciamo che y è inversamente proporzionale a x se xy=c o equivalentemente se y=c/x, con c come costante.

In entrambi i casi esiste quindi una proporzione che rimane costante (indice di un qualche tipo di legame tra i due valori), ma mentre nelle grandezze direttamente proporzionali all’aumentare di una grandezza, aumenta anche l’altra ed al diminuire di una grandezza, diminuisce anche l’altra; al contrario nelle grandezze inversamente proporzionali all’aumentare di una grandezza, diminuisce l’altra ed al diminuire di una grandezza, l’altra aumenta.

Grandezze su piano cartesiano

Possiamo facilmente notare se due quantità sono o meno direttamente proporzionali rappresentandole sul piano cartesiano come quello che vedete qui in basso. Disegniamo un piano cartesiano in cui i due assi rappresentano le due grandezze in questione: nel nostro caso, l’asse x delle ascisse indicherà la lunghezza del tratto percorso, mentre l’asse y delle ordinate rappresenterà il tempo impiegato a percorrere quel tratto. Riportiamo quindi i valori ottenuti nella tabella precedente sul piano cartesiano:

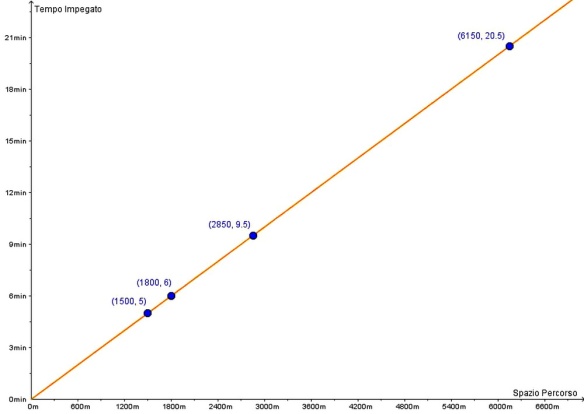
MEDICINA ONLINE ESEMPI DI VALORI GRANDEZZE DIRETTAMENTE PROPORZIONALI ASSE CARTESIANO VELOCITA ASCISSE ORDINATE.jpg

Per i quattro punti evidenziati passa una sola retta: grandezze direttamente proporzionali giacciono su una retta che passa per l’origine degli assi. La costante di proporzionalità tra le due grandezze rappresenta il coefficiente angolare della retta. Sussiste una fondamentale analogia tra grandezze direttamente proporzionali e le proporzioni. Infatti, se sappiamo che due grandezze AA e BB sono direttamente proporzionali, sappiamo che qualsiasi coppia di valori sta in un certo rapporto, o, appunto, in una certa proporzione. Supponiamo di avere due valori per la grandezza AA, che chiamiamo A1A1 e A2A2, ai quali corrispondono due valori per la grandezza BB, che chiamiamo B1B1 e B2B2. Se AA e BB sono direttamente proporzionali, i quattro valori soddisfano la proporzione:

A1 : B1 = A2 : B2

Grazie a questa proporzione e alle loro proprietà, sapendo che due grandezze sono tra loro direttamente proporzionali bastano tre valori qualunque per trovare il quarto, secondo il metodo generale di risoluzione delle proporzioni.

Nel piano cartesiano appena visto la retta cresce verso destra, puntando in alto a destra; in caso di valori inversamente proporzionali accadrebbe invece il contrario: decrescerebbe verso destra, puntando in basso a destra.

Esempi di grandezze inversamente proporzionali

Velocità e tempo necessario per coprire un dato percorso sono inversamente proporzionali:

all’aumentare della velocità, la meta viene raggiunta prima quindi diminuisce il tempo;
all’aumentare del tempo necessario per coprire una dato percorso, la velocità diminuisce.

Il numero di persone in una stanza e la quantità di superficie disponibile per ognuno sono inversamente proporzionali:

all’aumentare delle persone nella stanza, la quantità di superficie disponibile per ognuno diminuisce;
al diminuire delle persone nella stanza, la quantità di superficie disponibile per ognuno aumenta.

Il numero di persone che fanno un regalo in “comunità” e la quantità di denaro che ognuno dovrà sborsare:

all’aumentare delle persone che decidono di fare un regalo in comunità, meno soldi dovranno essere sborsati da ognuno;
al diminuire delle persone che decidono di fare un regalo in comunità, più soldi dovranno essere sborsati da ognuno.

Il numero di persone presenti ad una festa e la quantità di torta che ognuno potrà mangiare:

all’aumentare delle persone presenti alla festa, meno torta potrà essere mangiata da ognuno;
al diminuire delle persone presenti alla festa, più torta potrà essere mangiata da ognuno.

Esempi di grandezze direttamente proporzionali

La misura del lato di un poligono regolare e quella del suo perimetro sono direttamente proporzionali:

all’aumentare della misura del lato, aumenta quella del suo perimetro;
al diminuire della misura del lato, diminuisce quella del suo perimetro.

La misura del raggio di una circonferenza e quella del suo diametro sono direttamente proporzionali:

all’aumentare della misura del raggio, aumenta quella del suo diametro;
al diminuire della misura del raggio, diminuisce quella del suo diametro.

L’altezza di un rettangolo di base fissa e la sua area sono direttamente proporzionali:

all’aumentare dell’altezza, aumenta l’area;
al diminuire dell’altezza, diminuisce l’area.

La quantità di torta da preparare e quella delle quantità di uova necessarie per la sua preparazione sono direttamente proporzionali:

all’aumentare della quantità di torta, aumenta quella delle uova necessarie;
al diminuire della quantità di torta, diminuisce quella delle uova necessarie.

Direttamente ed inversamente proporzionale in medicina

Non necessariamente se due valori sono direttamente o inversamente proporzionali in “una direzione”, lo sono anche nella direzione contraria. Ad esempio nel corpo umano la secrezione di insulina e la glicemia sono inversamente proporzionali poiché:

all’aumentare della secrezione dell’ormone insulina, la glicemia diminuisce

In questo caso, però, il contrario è invece un esempio di valori direttamente proporzionali: all’aumentare della glicemia, aumenta anche la secrezione di insulina che continua ad aumentare fintanto aumenta la glicemia per poi diminuire quando la glicemia torna normale (meccanismo omeostatico di feedback negativo). Per approfondire, leggi anche: